PML uses UDP multicast packets to distribute resources from a single sender to
a (potentially very large) group of receivers. The receivers provide no
feedback to the sender whether they have received all the packets or not.
Because packet-loss is always to be expected, Forward Error Correction (FEC) is
required to prevent certain levels of packet-loss from impacting the complete
reception of the original data.
Reed-Solomon codes are used to perform the Forward Error Correction. In
short, when an original block of data of 100 bytes is encoded using FEC to 100
+ n bytes (where n can be chosen from 1 up to 100 bytes), all the 100 + n bytes
are transmitted. The receiver only has to receive any 100 of the bytes and the
FEC decoder can then re-construct the original 100 bytes.
Reed-Solomon encoding is currently only `fast' and practical at a symbol size
of 8 bits. This gives us a coding block of 2 ** 8 - 1 = 255 symbols that can be
decoded at a time. There is no point in sending these 255 symbols in one single
packet. The packet itself can (virtually) not be corrupted because of the
checksums in the IP and UDP headers. The only thing that can go wrong is that a
packet gets lost. If we put the 255 symbols in one single packet and the packet
is lost then this would cause a loss all symbols and ofcourse the decoder can't
handle the loss of that many symbols. We thus need a way to ensure that the
loss of a packet doesn't cause the loss of a large number of symbols in a
single coding block.
The way this is solved in PML is that we use a Forward Error Correction code
FEC() with 255 (= S = symbols in the coding block) UDP/IP packets with a
payload size P. We select an error correction capability E. We encode P coding
blocks of (S - E) symbols. We copy each symbol s in coded block FEC(p) to
packet s at position p. When all P blocks are encoded in the S packets then we
start sending the packets. Because a file is often larger then P * (S - E)
bytes we have to divide the file in segments of size P * S bytes. Each packet
that we send has indicated in its PMTP header what the segment number is. In
the PMTP header is also indicated the sequence number of the packet in the
segment. If we now lose a single packet then this causes a single erasure in
all P encoding blocks. But that's okay as long as we don't lose more then E out
of the S packets then the decoding function can handle the decode (if we
defined NROOTS as 8 so 8 packets may be lost out of the 255). Furthermore,
because we keep track of sequence numbers in the PMTP header we also now the
erasure location, so we can aid the decoder. In the decoder we wait until we
have received as much packets with a payload P as possible. We then check that
we have received sufficient packets for the decoder to work. If we do then we
copy each byte p from packet s to symbol s in coded block p. We then decode
each of the coded blocks and, if successful, write the coding block to disk. We
will be receiving packets in the receiver. Some of the packets that have been
sent will not be received or may be received out of order which we can tell by
looking at the sequence number in the PMTP header. We can also receive packets
belonging to the next segment before we have received all packets of the
current segment. Only when we've received all s packets then we can be sure
that there are no more packets to come for the current segment. But ofourse,
packets sometimes get lost. That's why we decide that if we have received
MAX_PACKETS_LOST packets from the new segment that we don't expect to receive
packets of the current segment anymore. We then start the decoding of the
current segment, write the segment to disk and make the new segment the current
segment.
This scheme is explained more elaborately below. We use in this example a
Reed-Solomon code FEC() with a symbol size of 8 resulting in S= 2^8-1= 255
coding symbols and E=8 error correction symbols. We can thus encode 255 - 8 =
247 symbols at a time. The decoding function will be indicated with FEC'(). In
this example we will use a P2P Multicast Transport (PMT) payload size of P =
1024 bytes
|
We split a file into different parts to support partial file sharing in P2P
networks
|
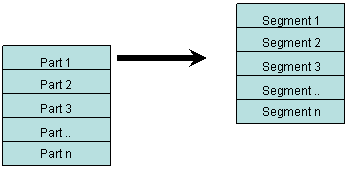
We split each part into multiple segments, with each segment being payload P
times S bytes (= 1024 * 247 = 252928).
|
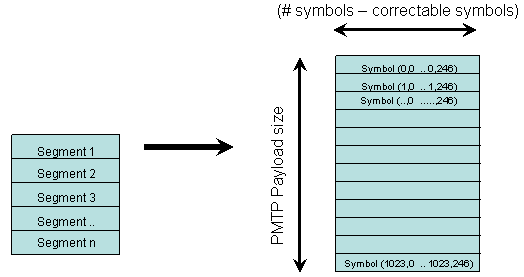
Each segment consists of P blocks of S (=247) symbols
|
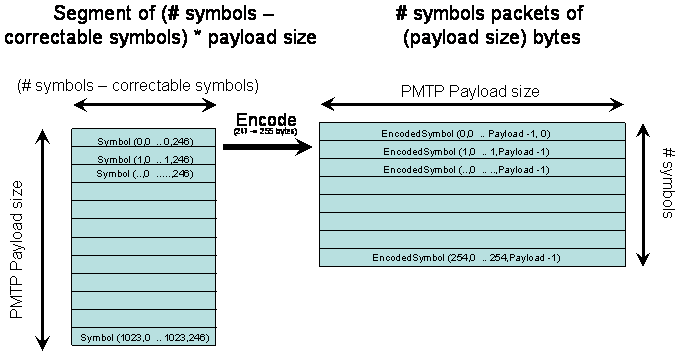
We encode each block b (0 <= b < P=1024) of S symbols resulting in FEC(b)
and we put each symbol s (0< = s < 255) of FEC(b) in position b of packet
s
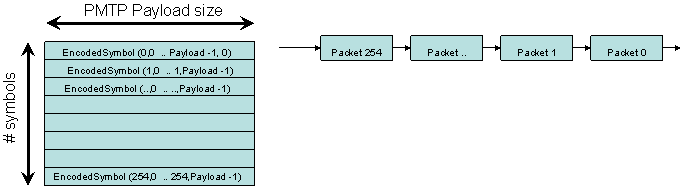
|
We send each of the S packets
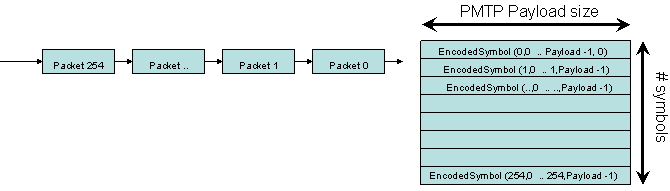
|
At the receiving side, we receive the S packets and put each byte b (0 <= b
< P) of packet s (0 <= s < 255) in in position s of block b

|
We decode each block b resulting in FEC'(b) and put the 247 original bytes into
an array
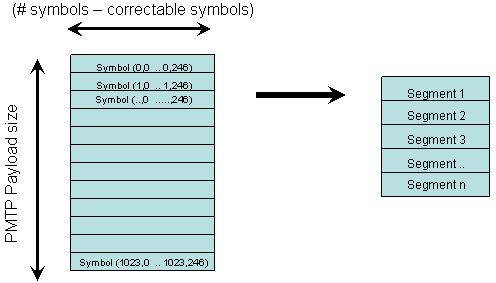
|
After we've decoded all packets of the segment, we can reconstruct the segment
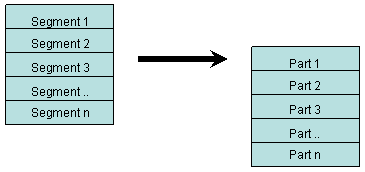
|
When we've got all the segments, we can recreate the part
|
When we've got all the parts, we can reconstruct the file